Chia đôi một góc
Câu hỏi
Phát biểu đơn giản
Cho một góc bất kỳ, làm thế nào để chia đôi góc đó chỉ sử dụng thước thẳng và compa?
Phát biểu chi tiết
Giả sử ta có ba điểm \(O\), \(A\) và \(B\) không thẳng hàng trên mặt phẳng Euclid. Ba điểm này xác định một góc \(x = \angle AOB\). Bài toán đặt ra là tìm điểm \(C\) sao cho tia \(OC\) chia đôi góc giữa tia \(OA\) và \(OB\), hay nói cách khác là sao cho
\[\angle AOC = \angle BOC = \frac{\angle AOB}{2} = \frac{x}{2}.\]Ở đây, ta chỉ quan tâm đến trường hợp \(0 < x < 180^\circ\). Nếu \(x = 0^\circ\) hoặc \(x = 180^\circ\), thì tia \(OC\) chính là tia \(OA\) hoặc tia \(OB\). Nếu \(x > 180^\circ\), ta có thể chia đôi góc phụ \(360^\circ - x\) thay vì góc chính \(x\) và sử dụng tia đối của tia \(OC\) làm tia chia đôi góc \(x\).
Để tìm được điểm \(C\), ta chỉ được sử dụng hai công cụ là thước thẳng và compa. Cụ thể, ta chỉ có thể thực hiện các thao tác dựng hình cơ bản sau:
- Chọn hai điểm \(A\) và \(B\) khác nhau bất kì. Vẽ một đường thẳng đi qua hai điểm bất kỳ \(A\) và \(B\). Đường thẳng này có thể kéo dài vô hạn về hai phía. Hãy hình dung việc đặt thước thẳng qua hai điểm \(A\) và \(B\), sau đó vẽ đường thẳng dọc theo cạnh thước.
- Chọn ba điểm \(A\), \(B\) và \(C\) không nhất thiết khác nhau bất kì. Vẽ một đường tròn với tâm tại điểm \(C\) và bán kính là khoảng cách giữa hai điểm \(A\) và \(B\). Hãy hình dung việc mở rộng compa cho đến ngang bằng khoảng cách giữa hai điểm \(A\) và \(B\), sau đó vẽ đường tròn với tâm tại \(C\).
- Thêm giao điểm giữa hai đường thẳng, hoặc giữa hai đường tròn, hoặc giữa một đường thẳng và một đường tròn vào tập hợp các điểm mà ta có thể sử dụng trong các bước tiếp theo.
Giải quyết
Phương pháp cổ điển
Có lẽ những ai đã biết về bài toán này cũng đều biết phương pháp cổ điển:
- Vẽ đường tròn tâm \(O\) và bán kính \(OB\).
- Đường tròn này giao tia \(OA\) tại điểm \(D\).
- Với cùng bán kính \(OB\), vẽ hai đường tròn tâm lần lượt tại \(D\) và \(B\). Hai đường tròn này giao nhau tại điểm \(C\).
- Vẽ tia \(OC\). Tia này sẽ chia đôi góc \(\angle AOB\).
Phương pháp này hoàn toàn đối xứng, tức là nếu ta đổi vai trò của hai điểm \(A\) và \(B\), ta vẫn thu được cùng một điểm \(C\).
Minh họa các bước trên như sau:
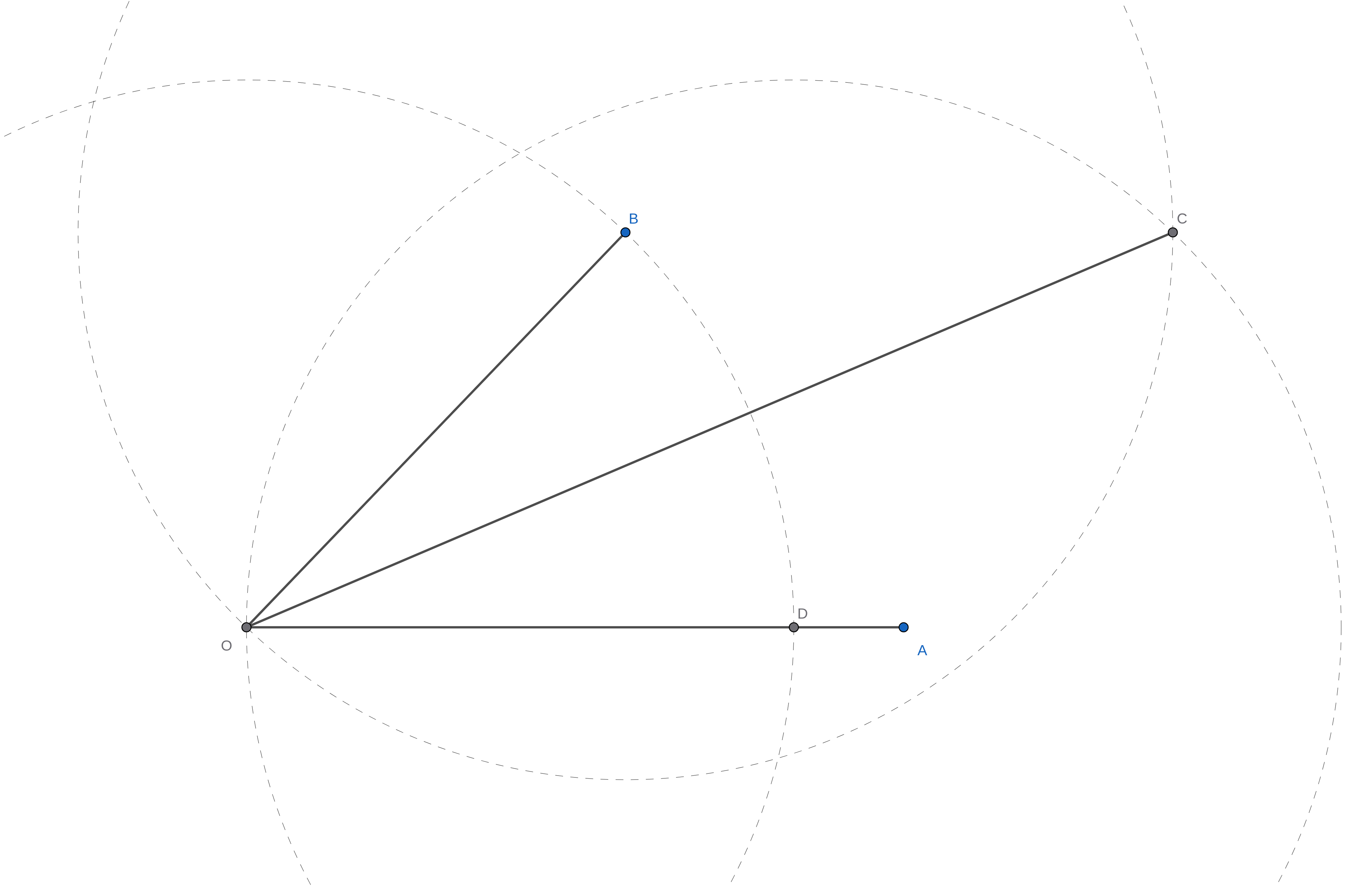
Việc chứng minh rằng tia \(OC\) chia đôi góc \(\angle AOB\) rất đơn giản, chỉ cần nhận thấy \(OBCD\) là một hình thoi (\(BC = BO = DO = DC\)).
Phương pháp kỳ lạ
Phương pháp ở trên rất đẹp và ngắn gọn, nhưng cá nhân mình lại thấy thiếu thú vị. Trong bài viết này, mình sẽ trình bày một phương pháp khác, phức tạp hơn cần thiết rất nhiều. Tuy nhiên, mình lại cho rằng đây là cách giải thú vị hơn, bởi vì nó sử dụng các công cụ đại số. Đây cũng là tiền đề cho các mở rộng về sau phân tích các bài toán dựng hình bằng thước thẳng và compa khác. (Thật ra là cố gắng bôi ra để có cái mà viết.)
Trước hết, để đơn giản hóa bài toán mà không làm mất tính tổng quát, ta có thể giả sử thêm:
- Điểm \(O\) là gốc tọa độ \((0,0)\).
- Điểm \(A\) tương ứng với điểm \((1,0)\).
- Điểm \(B\) nằm trên đường tròn đơn vị (tâm tại gốc tọa độ và bán kính bằng \(1\)). Điều này không làm mất tính tổng quát vì ta có thể xét giao điểm của tia \(OB\) với đường tròn đơn vị thay vì điểm \(B\) ban đầu.
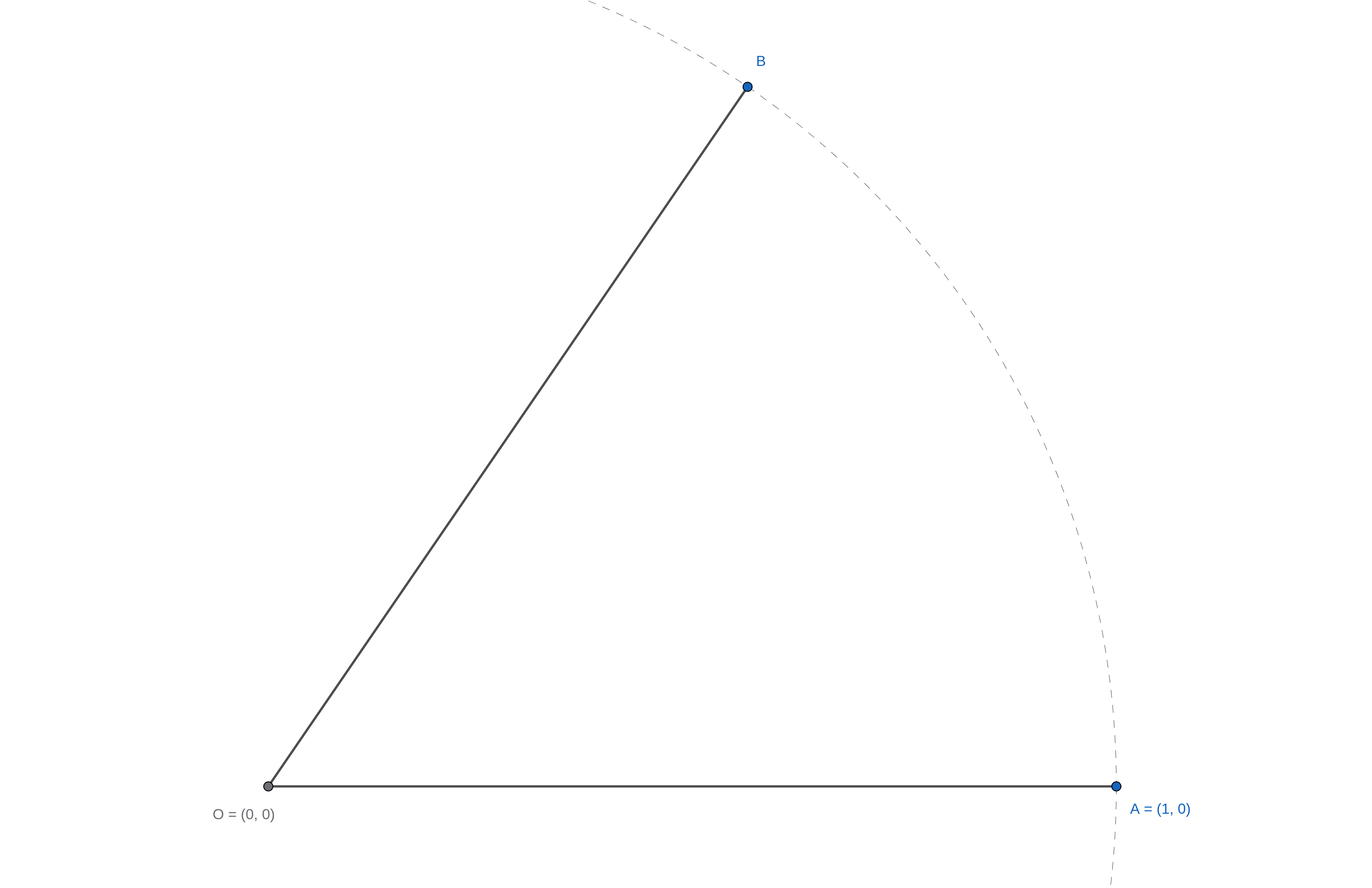
Với những giả sử này, ta biết được điểm \(B\) có tọa độ \((\cos x, \sin x)\). Đặc biệt hơn, ta cũng biết được điểm \(C\) cần tìm sẽ có tọa độ dạng \((\cos \frac{x}{2}, \sin \frac{x}{2})\). Câu hỏi lúc này trở thành: làm thế nào để dựng được điểm có tọa độ \((\cos \frac{x}{2}, \sin \frac{x}{2})\) chỉ sử dụng thước thẳng và compa, biết rằng ta đã có sẵn điểm \((1,0)\) và điểm \((\cos x, \sin x)\)?
Một số biến đổi đại số sử dụng các công thức lượng giác cơ bản sẽ cho ta biết được rằng
\[\cos \frac{x}{2} = \sqrt{\frac{1 + \cos x}{2}}\]Do đó, để dựng được điểm \(C\), ta chỉ cần dựng được điểm
\[C_x = \left(\sqrt{\frac{1 + \cos x}{2}}, 0\right)\]và dóng một đường thẳng từ điểm \(C_x\) vuông góc với \(OA\) và giao với đường tròn đơn vị để tìm được điểm \(C\) (ta sẽ sớm thấy việc này là khả thi với các thao tác dựng hình cơ bản nêu trên). Câu hỏi lúc này trở thành: làm thế nào để dựng được điểm \(C_x\)?
Ta nhận thấy hoành độ của \(C_x\) là kết quả của việc thực hiện các phép toán đại số sau:
- Bắt đầu từ \(\cos x\) (đây là hoành độ của điểm \(B\)).
- Cộng \(1\) (độ dài của đoạn \(OA\)) vào \(\cos x\) để được \(1 + \cos x\).
- Chia kết quả ở bước 2 cho \(2\) để được \(\frac{1 + \cos x}{2}\).
- Lấy căn bậc hai của kết quả ở bước 3 để được \(\sqrt{\frac{1 + \cos x}{2}}\).
Từ đó, ta sẽ lần lượt tìm cách dựng được các điểm tương ứng với kết quả của từng bước trên. Cụ thể, quy trình dựng sẽ gồm các bước sau
- Dóng đường thẳng từ điểm \(B\) vuông góc \(OA\) để thu được giao điểm \(B_x\) với \(OA\). Điểm \(B_x\) có hoành độ \(\cos x\).
- Vẽ đường tròn tâm \(B_x\) và bán kính \(OA = 1\) để thu được giao điểm \(D\) với tia \(OA\). Điểm \(D\) có hoành độ \(1 + \cos x\).
- Lấy trung điểm \(E\) của đoạn thẳng \(OD\). Điểm \(E\) có hoành độ \(\frac{1 + \cos x}{2}\).
- Tìm điểm \(C_x\) trên tia \(OE\) có khoảng cách tới \(O\) bằng căn bậc hai của \(OE\). Điểm \(C_x\) có hoành độ \(\sqrt{\frac{1 + \cos x}{2}}\) như mong muốn.
Minh họa các bước trên như sau:
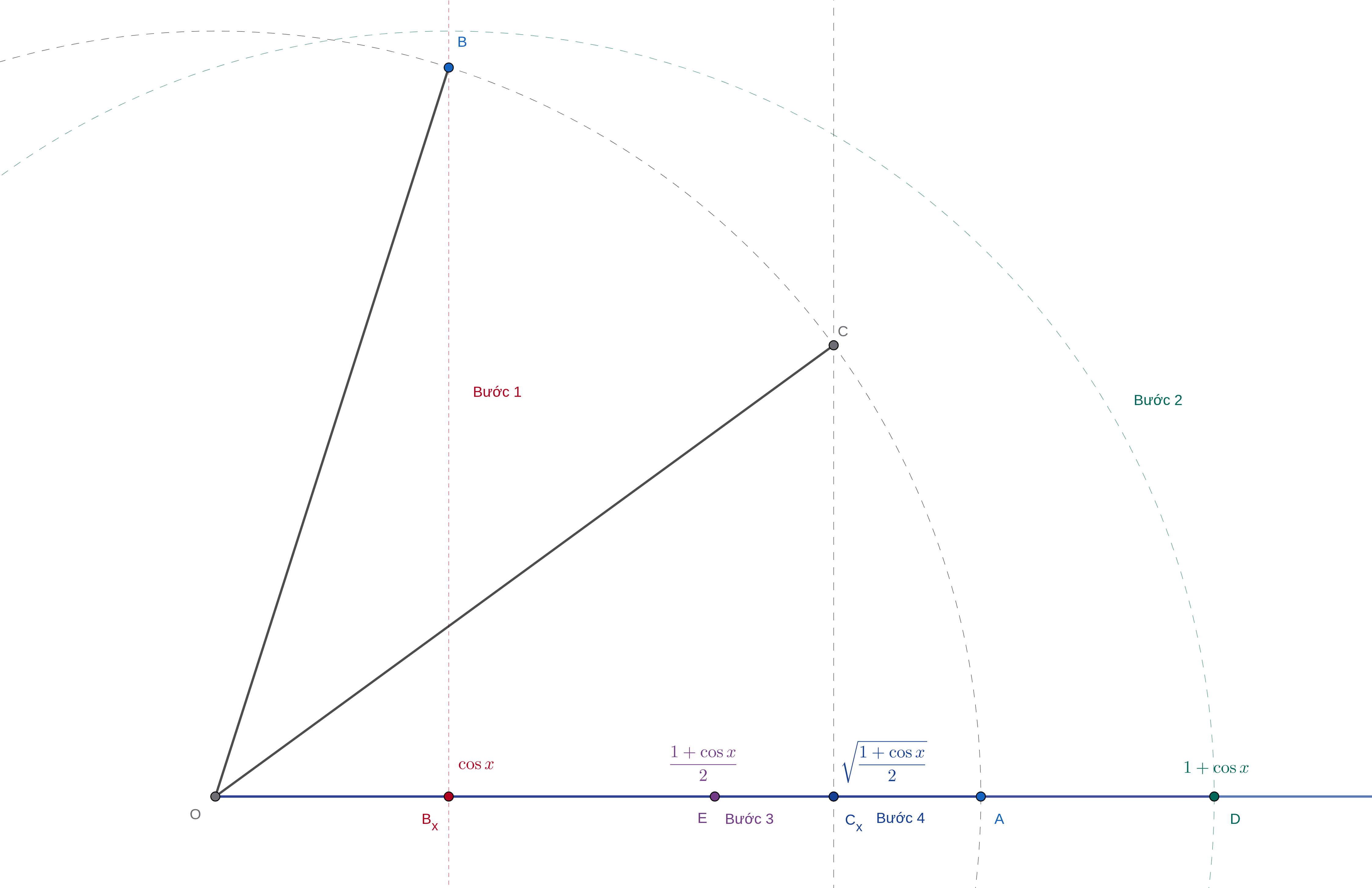
Bạn đọc tinh ý sẽ ngay lập tức nhận ra vấn đề ở các bước 1, 3, và 4. Bởi vì các bước này đều yêu cầu nhiều hơn một thao tác dựng hình cơ bản. Cụ thể,
- bước 1 (và cả bước cuối cùng sau khi đã dựng được \(C_x\)) yêu cầu thao tác “dóng từ một điểm đường thẳng vuông góc với đường thẳng khác”,
- bước 3 yêu cầu thao tác “tìm trung điểm của đoạn thẳng”, và
- bước 4 yêu cầu thao tác “lấy căn bậc hai độ dài của đoạn thẳng”.
Phần tiếp theo của bài viết sẽ trình bày cách thực hiện các phép dựng hình này chỉ sử dụng các thao tác dựng hình cơ bản đã nêu ở phần đầu.
Dóng từ một điểm đường thẳng vuông góc với đường thẳng khác
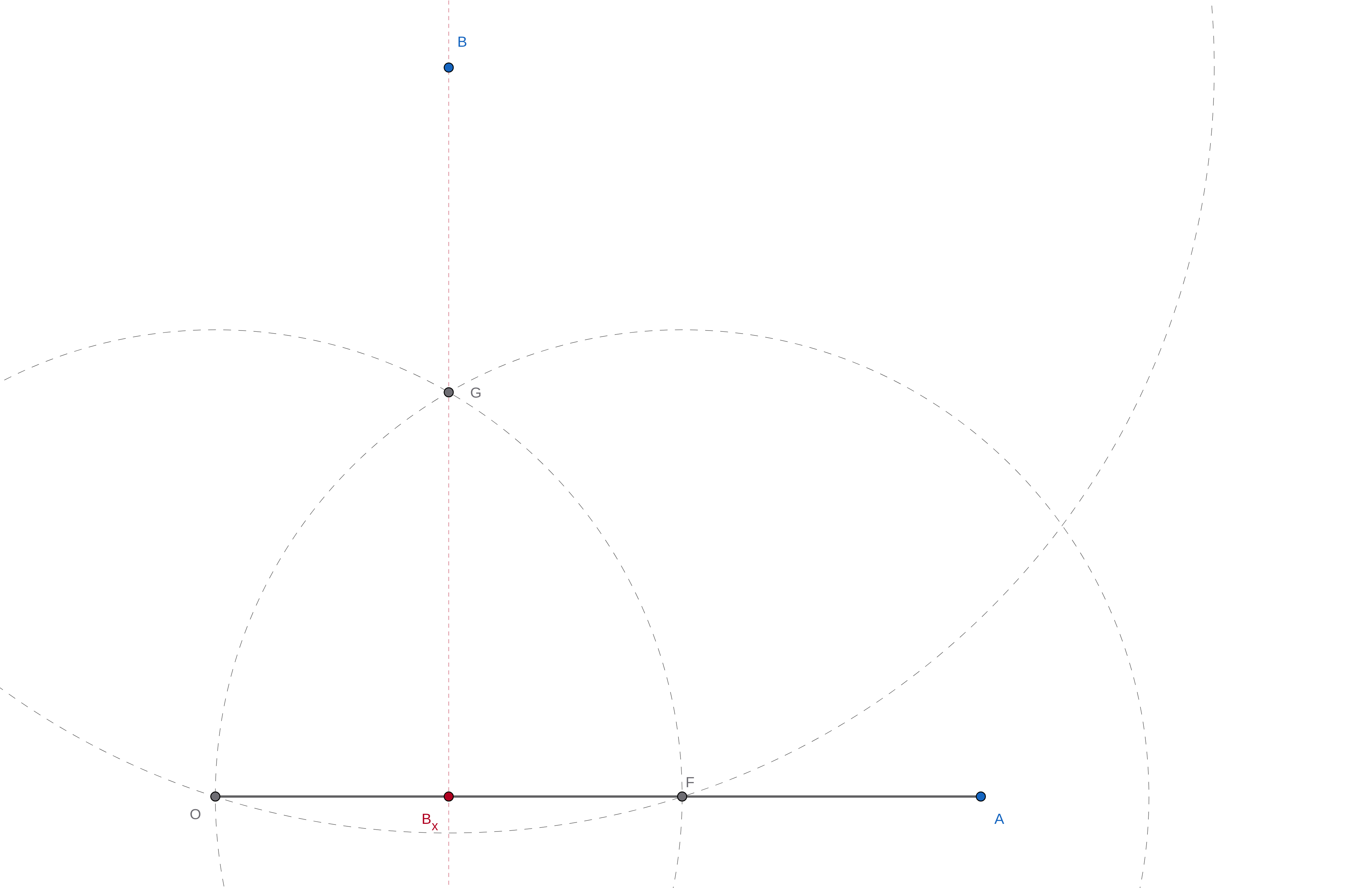
Ta xét cụ thể trường hợp cần dóng từ điểm \(B\) vuông góc với đường thẳng \(OA\). Để làm được điều này, ta thực hiện các bước sau:
- Vẽ đường tròn tâm \(B\) và bán kính \(BO\) để thu được giao điểm \(F\) với đường thẳng \(OA\).
- Với cùng bán kính \(OF\), vẽ hai đường tròn tâm lần lượt tại \(O\) và \(F\). Hai đường tròn này giao nhau tại điểm \(G\) (và một điểm \(G'\) khác).
- Vẽ đường thẳng \(BG\). Đây chính là đường thẳng cần tìm.
Ta có thể dễ dàng chứng minh rằng đường thẳng \(BG\) vuông góc với đường thẳng \(OA\) bằng cách nhận thấy tứ giác \(OGFG'\) là hình thoi (\(OG = OF = FG = FG'\)) và việc \(BO = BF\) cho thấy \(B\) nằm trên đường trung trực của đoạn thẳng \(OF\), chính là \(GG'\).
Tìm trung điểm của đoạn thẳng
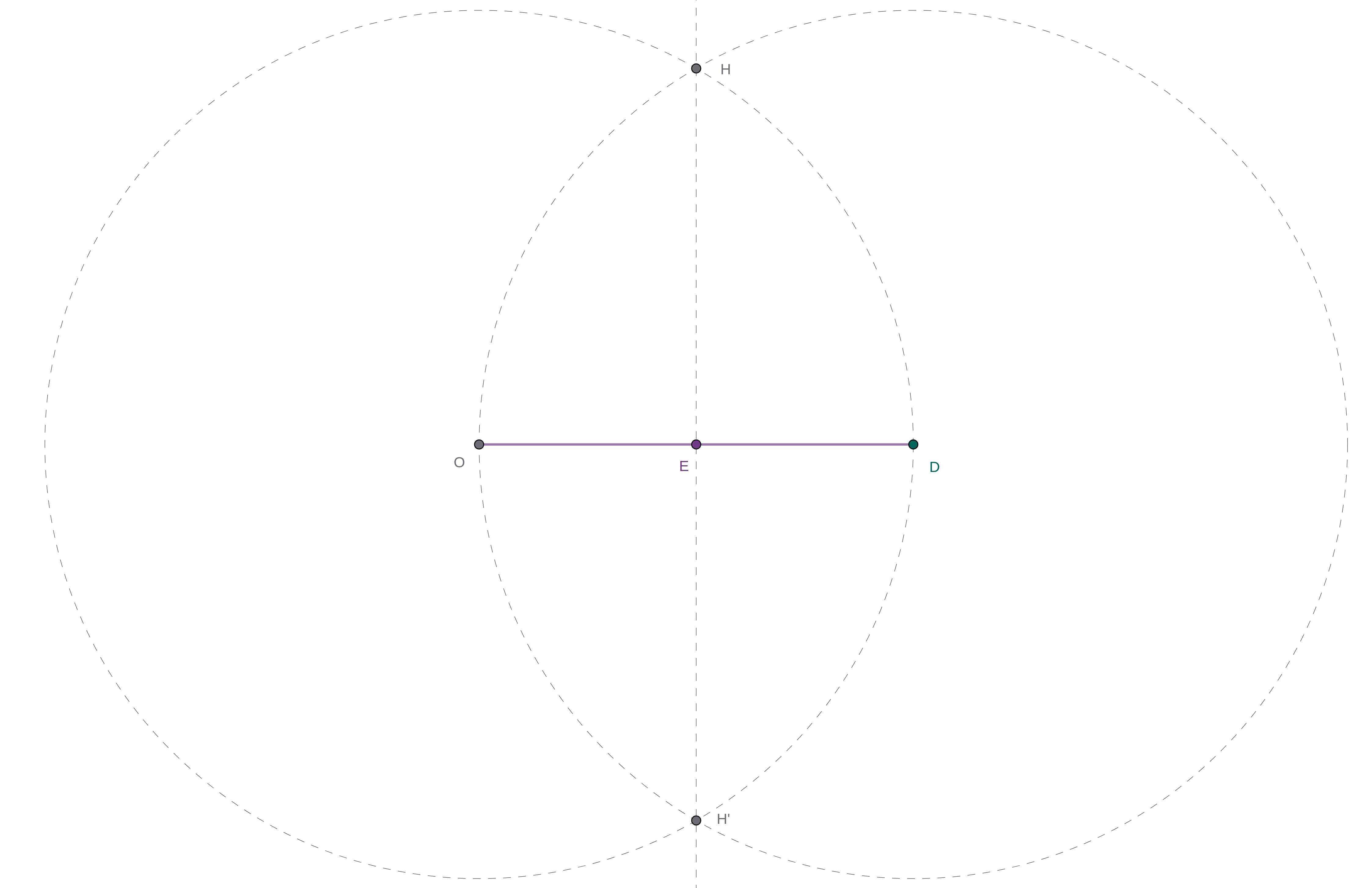
Ta xét cụ thể trường hợp cần tìm trung điểm của đoạn thẳng \(OD\). Để làm được điều này, ta thực hiện các bước sau:
- Với cùng bán kính \(OD\), vẽ hai đường tròn tâm lần lượt tại \(O\) và \(D\). Hai đường tròn này giao nhau tại điểm \(H\) (và một điểm \(H'\) khác).
- Vẽ đường thẳng \(HH'\). Giao điểm \(E\) của đường thẳng này với đoạn thẳng \(OD\) chính là trung điểm cần tìm.
Tương tự như trên, ta có thể dễ dàng chứng minh rằng \(E\) là trung điểm của đoạn thẳng \(OD\) bằng cách nhận thấy tứ giác \(OHH'D\) là hình thoi (\(OH = OD = DH = DH'\)).
Lấy căn bậc hai độ dài của đoạn thẳng
Đây có lẽ là thao tác phức tạp nhất và cũng là thao tác thú vị nhất. Việc ta có thể thực hiện thao tác này cho thấy ta có thể tính được căn bậc hai của một số cho trước chỉ sử dụng các phép dựng hình cơ bản bằng thước thẳng và compa. Trong phần này, ta chỉ xét việc lấy căn bậc hai của một số thực dương, nhưng ta sẽ dễ dàng mở rộng sang việc lấy căn bậc hai của số phức trong phần mở rộng tiếp theo.
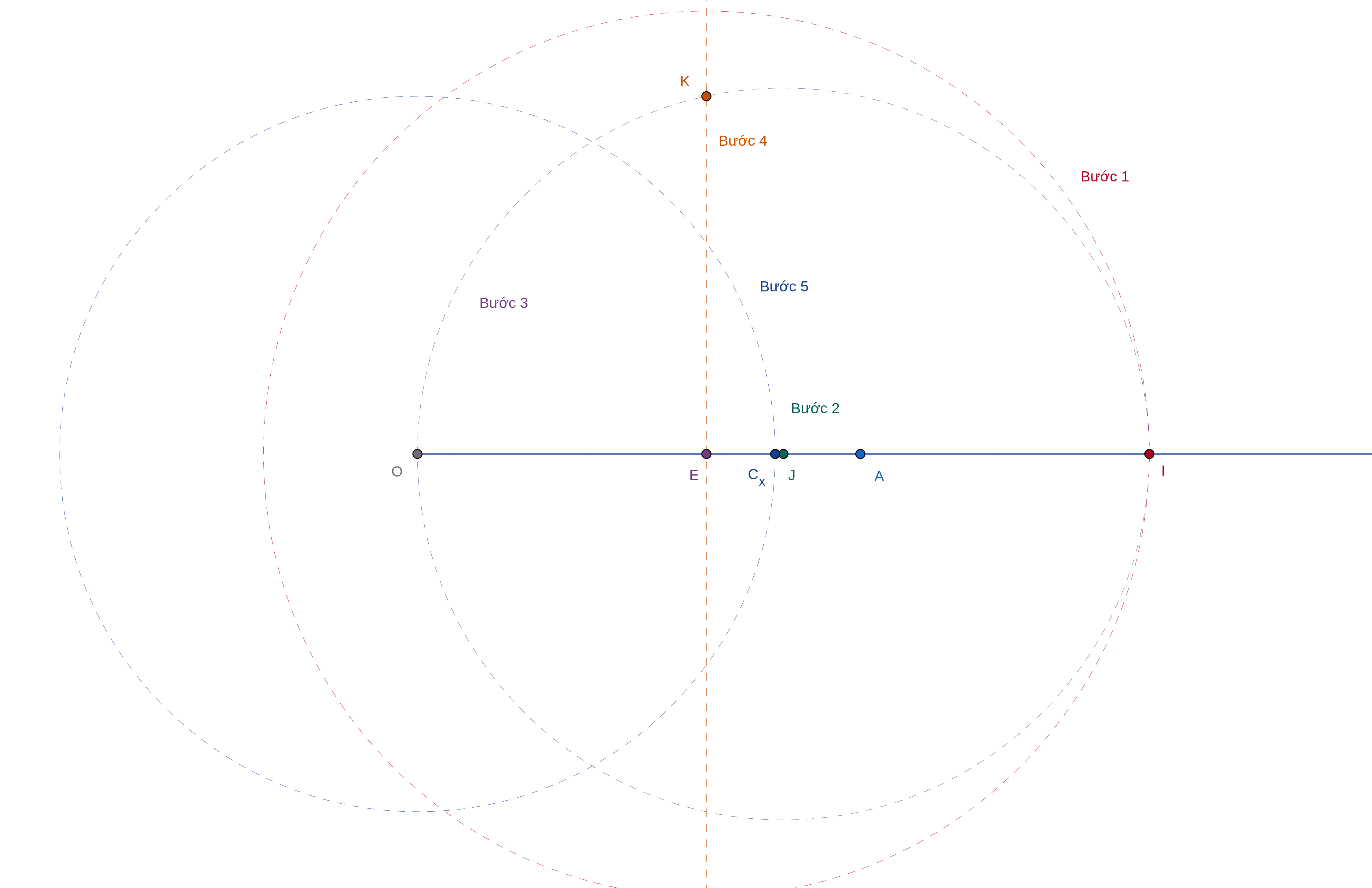
Gọi \(c > 0\) là độ dài của đoạn thẳng \(OE\). Ta xét cụ thể trường hợp cần tìm điểm \(C_x\) trên tia \(OE\) sao cho độ dài \(OC_x\) là \(\sqrt{c}\). Để làm được điều này, ta thực hiện các bước sau:
- Vẽ đường tròn tâm \(E\) với bán kính \(OA = 1\) để thu được giao điểm \(I\) với tia \(OE\).
- Lấy trung điểm \(J\) của đoạn thẳng \(OI\) (sử dụng phương pháp đã nêu ở phần trước).
- Vẽ đường tròn tâm \(J\) với bán kính \(JO\).
- Dóng từ điểm \(E\) vuông góc với đường thẳng \(OI\) để thu được giao điểm \(K\) với đường tròn tâm \(J\) ở Bước 3 (sử dụng phương pháp đã nêu ở phần trước).
- Đoạn thẳng \(EK\) chính là đoạn thẳng có độ dài \(\sqrt{c}\) như mong muốn. Do đó, điểm \(C_x\) chính là giao điểm của tia \(OE\) với đường tròn tâm \(O\) và bán kính \(EK\).
Thực tế, đây cũng chính là cách để tìm đoạn thẳng có độ dài là trung bình hình học của hai độ dài cho trước (ở đây là \(c\) và \(1\)). Việc chứng minh rằng \(EK = \sqrt{c}\) dựa trên đẳng thức \(EK^2 = EO \cdot EI = c \cdot 1 = c\) (\(EK\) vuông góc \(OI\)) của \(\Delta OKI\) vuông tại \(K\) (\(OI\) là đường kính hình tròn tâm \(J\)).
Mở rộng
Tính căn bậc hai của một số phức
Như đã gợi ý ở trên, ta không bị giới hạn ở việc lấy căn của đoạn thẳng (số thực), mà còn có thể lấy căn của số phức chỉ sử dụng các phép dựng hình cơ bản. Nói đúng hơn, nhờ vào khả năng lấy căn số thực mà ta có thể lấy căn số phức chỉ với thước thẳng và compa.
Xét số phức \(z = re^{ix}\) với \(r \geq 0\) và \(0^\circ < x < 180^\circ\) là góc pha của \(z\). Số phức này ứng với điểm \(B'\) có tọa độ \((r\cos x, r\sin x)\) trong mặt phẳng Euclid. Căn bậc hai của \(z\) được định nghĩa là số phức \(w = \sqrt{r}e^{ix/2}\), ứng với điểm có tọa độ
\[\left(\sqrt{r}\cos \frac{x}{2}, \sqrt{r}\sin \frac{x}{2}\right)\]Có thể thấy rằng để dựng được điểm ứng với \(w\), ta chỉ cần thực hiện hai bước:
- Dựng tia \(OC\) chia đôi góc \(\angle AOB'\) (theo một trong hai phương pháp đã nêu ở phần trước, tất nhiên là ưu tiên phương pháp cổ điển).
- Dựng điểm \(C'\) trên tia \(OC\) sao cho độ dài \(OC' = \sqrt{r}\) (sử dụng phương pháp đã nêu ở phần trước).
Dễ thấy điểm \(C'\) chính là điểm ứng với số phức \(w\).
Kết quả này cho thấy chỉ với thước thẳng và compa, ta có thể thực hiện phép lấy căn bậc hai trên tập hợp số phức. Điều này dẫn đến nhiều hệ quả thú vị trong nghiên cứu về các bài toán dựng hình bằng thước thẳng và compa khác, chẳng hạn như việc xác định có thể hay không thể thực hiện được một số phép dựng hình nhất định. Việc xác định này tương đương với việc xác định xem các số phức liên quan có thể thu được từ các số phức ban đầu thông qua các phép toán cộng trừ nhân chia và phép lấy căn bậc hai hay không.
Chia ba một góc
Câu hỏi tiếp theo mà ta có thể đặt ra là: làm thế nào để chia ba một góc chỉ sử dụng thước thẳng và compa? Hay nói cách khác, làm thế nào để tìm điểm \(C\) sao cho tia \(OC\) tạo thành góc \(\angle AOC = x / 3\)? Tất nhiên là việc chia ba một số góc đặc biệt như \(90^\circ\) hay \(135^\circ\) (tương ứng với dựng góc \(30^\circ\) hay \(45^\circ\)) thì việc chia ba là khả thi. Thế nhưng các nhà toán học ngày xưa đã không thể tìm được một phương pháp tổng quát để làm việc này cho mọi góc cho trước. Ngày nay, ta biết một phương pháp tổng quát như vậy không thể tồn tại.
Nói đơn giản, lý do nằm ở chỗ, giống như cách mà việc chia đôi một góc là tương đương với việc lấy căn bậc hai, việc chia ba một góc lại tương đương với việc lấy căn bậc ba. Tuy nhiên, không phải căn bậc ba nào cũng có thể được tính chỉ với các phép toán cộng trừ nhân chia và phép lấy căn bậc hai (ví dụ \(\sqrt[3]{2}\) không thể biểu diễn bằng các phép toán đó). Tương ứng, không phải mọi góc đều có thể chia ba chỉ với thước thẳng và compa. Chứng minh chặt chẽ của kết quả này sử dụng các công cụ đại số trừu tượng và nằm ngoài phạm vi của bài viết này, nhưng bạn đọc quan tâm có thể tham khảo thêm trong các tài liệu về lý thuyết trường và đa thức.
Tham khảo
- Lecture Notes 3: Field theory, MATH 500: Abstract Algebra, Fall 2025, University of Illinois Urbana-Champaign
- Compass and Straightedge Construction of Geometric Mean - planetmath.org