Chọn ngẫu nhiên điểm trong hình tròn

Câu hỏi

Làm thế nào để chọn ngẫu nhiêu đều một điểm trong hình tròn?

Tiếp cận

Không mất tính tổng quát, xét hình tròn tâm \(O(0, 0)\), bán kính \(R = 1\). Ta cần sinh điểm ngẫu nhiên thỏa yêu cầu đề bài.

Cách không đúng

Một cách ngây thơ, sẽ có người nghĩ đến việc sinh ngẫu nhiên trong hệ tọa độ cực trước bằng cách xét hai biến ngẫu nhiên

• \(D\): khoảng cách đến tâm hình tròn, phân bố đều trên \([0, 1]\), hay \(D \sim U(0, 1)\),
• \(\Theta\): góc giữa \(\vec{OA}\) và \(\vec{Ox}\), phân bố đều trên \([0, 2\pi]\), hay \(\Theta \sim U(0, 2\pi)\).

Từ đó, hoành độ \(X\) và tung độ \(Y\) (là hai biến ngẫu nhiên) có thể tính được dựa trên công thức biến đổi từ hệ tọa độ cực sang hệ tọa độ Oxy:

\[X = D \cos \Theta, \;\; Y = D \sin \Theta.\]

Mã nguồn Python cho phương pháp này là như sau

def gen1(N):
    # Random samples d's from U(0, 1)
    D = np.random.rand(N)

    # Random samples theta's from U(0, 2 * pi)
    Theta = np.random.rand(N) * 2 * np.pi

    # Transformation from polar to Cartesian coordinates
    X = D * np.cos(Theta)
    Y = D * np.sin(Theta)
    return X, Y

Làm theo cách này, kết quả thu được sẽ như hình dưới (\(N = 5000\)).

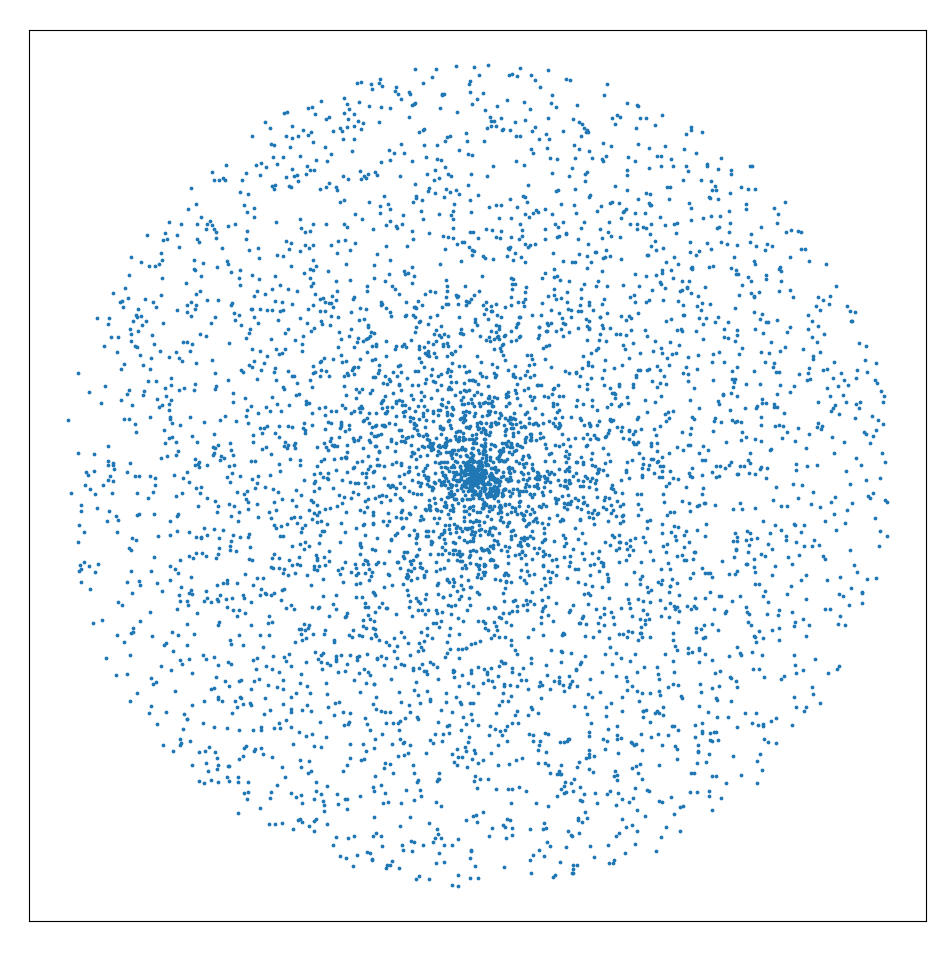
Nếu để ý kỹ, mọi người sẽ nhận ra có một vấn đề với cách tiếp cận này: Có vẻ như là các điểm được chọn co cụm về tâm nhiều hơn.

Tại sao lại có hiện tượng này? Rõ ràng là chúng ta đã chọn khoảng cách đến tâm là một phân bố đều rồi mà. Đổi góc nhìn một chút, hãy thử xét ví dụ thế này: Xét hai vùng A và B tương ứng là vùng chứa các điểm có khoảng cách đén tâm hình tròn là \([0.1, 0.2]\) và \([0.8, 0.9]\). Xác suất điểm được chọn đến từng vùng A và vùng B đều là \(0.1 = P(0.1 \leq D \leq 0.2) = P(0.8 \leq D \leq 0.9)\). Tuy nhiên, diện tích của vùng A là \(\pi 0.2^2 - \pi 0.1^2 = 0.03\pi\), nhỏ hơn nhiều so với \(0.17\pi\) của vùng B. Nói cách khác, vùng A gần tâm hơn, diện tích nhỏ hơn, nhưng lại có cùng xác suất điểm được chọn rơi vào so với vùng B. Nói cách khác, điểm được chọn có xác suất rơi vào hai vùng là như nhau, nhưng do vùng A có diện tích bé hơn nên mật độ điểm ở đây dày đặc hơn vùng B.

Cụ thể hơn, ta có hàm mật độ

\[f_{(D, \Theta)}(d, \theta) = f_D(d)f_\Theta(\theta) = \left\{ \begin{array}{ll} \dfrac{1}{2\pi} & d \in [0, 1], \theta \in [0, 2\pi) \\ 0 & \text{khác} \end{array} \right. .\]

Trong đó, dấu \(=\) đầu tiên là do \(R\) và \(\Theta\) độc lập với nhau.

Sử dụng công thức đổi biến với công thức biến đổi hệ tọa độ, ta có

\[f_{(X, Y)}(x, y) = f_{(D, \Theta)}(d, \theta) \left| \begin{array}{cc} \dfrac{\partial x}{\partial d} & \dfrac{\partial x}{\partial \theta} \\ \dfrac{\partial y}{\partial d} & \dfrac{\partial y}{\partial \theta} \end{array} \right|^{-1} = f_{(D, \Theta)}(d, \theta) \left| \begin{array}{cc} \cos \theta & -d \sin \theta \\ \sin \theta & d \cos \theta \end{array} \right|^{-1}\] \[= \dfrac{1}{d} f_{(D, \Theta)}(d, \theta) = \left\{ \begin{array}{ll} \dfrac{1}{2\pi \sqrt{x^2 + y^2}} & x^2 + y^2 \leq 1 \\ 0 & \text{khác} \end{array} \right. .\]

Có thể thấy mật độ điểm được chọn sẽ giảm đi khi càng ra xa tâm hình tròn (\(x^2 + y^2\) càng lớn). Ngoài ra, cũng có thể thấy rõ là cách tiếp cận này không thỏa yêu cầu bài toán, vốn yêu cầu hàm mật độ phải là \(\pi^{-1}\) bên trong hình tròn.

Lấy mẫu nghịch đảo

Đến đây, có thể mọi người đã định hình một số cách tiếp cận trong đầu rồi. Mấu chốt ở đây là chúng ta không thể lấy phân bố \(R\), hay khoảng cách đến tâm, một cách đều trên \([0, 1]\) được, mà những điểm ở xa tâm sẽ phải được “ưu ái” hơn để cân bằng với phần diện tích.

Cụ thể, một cách trực quan, ta có

\[F_D(d) = P(D \leq d) = \left\{ \begin{array}{ll} 0 & d < 0 \\ \dfrac{\pi d^2}{\pi R^2} & 0 \leq d < R\\ 1 & 1 \leq d \end{array} \right. = \left\{ \begin{array}{ll} 0 & d < 0 \\ d^2 & 0 \leq d \leq 1\\ 1 & 1 < d \end{array} \right. .\]

Như vậy, hàm mật độ của $D$ sẽ là

\[f_D(d) = \left\{ \begin{array}{ll} 2d & 0 \leq d \leq 1 \\ 0 & \text{khác} \end{array} \right. .\]

Ở đây, nhận xét \(P(D \leq d)\) bằng tỉ lệ diện tích hai hình tròn đồng tâm bán kính $d$ và $R$ thực chất là một nhận xét cảm tính. Ta cũng sẽ đi đến kết luận tương tự khi xét

\[f_D(d) = \dfrac{f_{(D, \Theta)}(d, \theta)}{f_\Theta(\theta)} = d \dfrac{f_{(X, Y)}(x, y)}{f_\Theta(\theta)} = \left\{ \begin{array}{ll} d \dfrac{1}{\pi} 2\pi & 0 \leq d \leq 1 \\ 0 & \text{khác} \end{array} \right. .\]

Câu hỏi được đặt ra bây giờ là: làm sao để lấy mẫu ngẫu nhiên từ phân bố của \(D\) được mô tả ở trên? Ở đây, hàm phân bố tích lũy của phân bố này có một tính chất đặc biệt: nó khả nghịch trên \([0, 1]\). Cụ thể, nghịch đảo của nó trên đoạn này là

\[F_D^{-1}(y) = \sqrt{F_D(y)}\]

Do đó, ta có thể ứng dụng phương pháp lấy mẫu như sau (thường gọi là lấy mẫu nghịch đảo, inverse sampling):

1. Lấy ngẫu nhiên $v$ từ \(U(0, 1)\)
2. Tính \(d = F_D^{-1}(v) = \sqrt{F_D(v)}\), đây chính là giá trị cần tìm

Tại sao phương pháp này lại hoạt động? Xét \(V \sim U(0, 1)\) và \(T = F_{D}^{-1}(V)\). Với mọi \(t\), có

\[F_T(t) = P(T \leq t) = P(F_{D}^{-1}(V) \leq t) = P(V \leq F_{D}(t)) = F_{V}(F_{D}(t)) = F_D(t)\]

Do đó, \(D\) và \(T = F_{D}^{-1}(V)\) có cùng phân bố.

Mã nguồn Python của cách tiếp cận này là như sau:

def gen2(N):
    # Random sample v's from U(0, 1)
    V = np.random.rand(N)
    # Calculate F_D^{-1}(v)
    D = np.sqrt(V)

    # Random samples theta's from U(0, 2 * pi)
    Theta = np.random.rand(N) * 2 * np.pi

    # Transformation from polar to Cartesian coordinates
    X = D * np.cos(Theta)
    Y = D * np.sin(Theta)
    return X, Y

Kết quả thu được như hình bên dưới (\(N = 5000\)).

Lấy mẫu từ chối

Phần này xin chỉ ra một cách tiếp cận theo tư tưởng lấy mẫu từ chối (rejection sampling). Ý tưởng ở đây rất đơn giản:

1. Lấy ngẫu nhiên \(x, y\) từ \(U(-1, 1)\)
2. Nếu \(x^2 + y^2 \leq 1\) (nằm trong hình tròn), ta nhận điểm đó. Ngược lại, lặp lại từ Bước 1.

Mã nguồn Python của cách tiếp cận này như sau (đã có thay đổi nhằm tăng tốc độ).

def gen3(N):
     points = 2 * np.random.rand(2, N) - 1
     accepted = ((points ** 2).sum(0) <= 1)
     while accepted.sum() < N:
         points[:, ~accepted] = 2 * np.random.rand(2, N - accepted.sum()) - 1
         accepted = ((points ** 2).sum(0) <= 1)
     return points[0], points[1]

Có thể thấy cách này có điểm yếu ở việc phải kiểm tra xem điểm sinh ra có bị từ chối hay không, do đó sẽ có một số lần lấy mẫu thừa ra. Cụ thể, trong trường hợp này khả năng bị từ chối là \(p=1-\pi/4 \approx 0.2146\). Ngoài ra, nó cũng khó khăn trong việc vectorize, khác với cách trên.